Математическое моделирование ламинарного течения

несжимаемой жидкости в трубах.

 Рассмотрим установившийся ламинарный поток в круглой цилиндри­ческой трубе, предположив линии тока прямыми, параллельными оси трубы (см. рис. 6), Будем рассматривать стационарный процесс, для которого

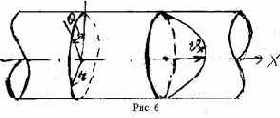
Предположим также, что среда несжимаема т.е. r=const. Кроме того, будем считать, что скорость потока и профиль скоростей не зависят от продольной координаты. Это так называемое стабилизированное движение, имеющее место в цилиндрической трубе на значительном расстоянии от входа. Следовательно, если направление движения совпадает с  осью Х, то проекции скоростей на оси y и z будут равны нулю:

.

Используя уравнение неразрывности для несжимаемой жидкости:

 получаем, что  и , следовательно, скорость в трубе не зависит от координаты X (условие стабилизированного течения), т.е. ux=ux(y,z) = u(y,z).

Тогда уравнения движения Навье - Стокса вязкой несжимаемой жидкости, имеющие вид:

а) в векторной форме

б) в проекциях на оси декартовых координат:

после подстановки значений

;

  ux=uz=0;

 (т.е. ); 

 (т.е. );

ux=u;  

и отбрасывания внешних сил Fx =Fy =Fz =0 преобразуются к виду:

Из этих уравнений следует:

1) величина давления не зависит от поперечных координат y и z и есть функция только координаты x, т.е. в частности, в круглой трубе давление меняется только вдоль оси, а, следовательно, постоянно в каж­дом сечении и не зависит от радиуса r ;

2) так как левая часть первого уравнения зависит только от у и  z, а правая часть не зависит  ни от у, ни от  z, то следовательно, правая и левая части этого уравнения должны быть равны одной и той же постоянной величине, т.е.

Таким образом, уравнение Навье - Стокса для стабилизированного движения жидкости в цилиндрической трубе вдоль оси X будет иметь вид:

 (1.32)

Если прямоугольную систему координат заменить на цилиндрическую, в которой x=x, y=r*cos(q); z= r*sin(q), то уравнение (1.32) примет  вид:

. (1.33)

Предполагая, что поток в трубе обладает осевой симметрией, заключаем, что все параметры не зависят от переменной q, т.е.

и .
Тогда:

 .

Так как  , то уравнение Навье - Стокса перепишется в виде:

.

Выполним последовательно двойное интегрирование.

После первого интегрирования получим:

 или .

Проинтегрируем еще раз:  (1.34)

Постоянные интегрирования С1 и С2 определяются из граничных условий. Для круглой трубы с радиусом  R  они могут  быть записаны так: при  r=R  (внутренний радиус трубы) скорость   u=0; при   r=0   скорость u - конечная величина.

Так как скорость потока в трубе должна иметь конечное значение (или нулевое при r=R ), а при  r® 0 формула (1.34) дает бесконечное значение скорости на оси, то физически реальный результат получим лишь при  C1 = 0. Используя первое граничное условие, найдем:

 и тогда   (1.35)

Таким образом, для круглой трубы имеем параболическое распределение скоростей по сечению (рис. 7).

На оси трубы, т.е. при r=0, скорость потока достигает максимального значения:

.

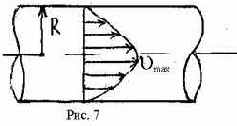 Тогда

или в безразмерном виде

.

Очевидно, что пространственная эпюра скоростей представляет собой параболоид вращения с основанием pR2 и высотой umax. Для цилиндрической трубы можно записать

,

где Dp - перепад давления в трубе длиной l.

Определим среднюю расходную и максимальную скорости в круглой трубе. Объемный расход жидкости равен:



Этот результат получается следующим образом:

.

Тогда

Поскольку расход Q связан со средней скоростью формулой , то , т.е. при ламинарном режиме течения в круглой трубе максимальная скорость жидкости в двое больше средней. Это очень важное свойство ламинарного установившегося движения жидкости в круглой трубе. Отсюда:

,  ,  .

Перепад давлений на участке трубы длиной l определяется как

,

где D - внутренний диаметр трубы.

Это формула Пуазейля, исследовавшего законы движения крови по капиллярным сосудам.

С другой стороны, для установившегося движения в цилиндрических трубах перепад давления определяется по формуле Дарси - Вейсбаха:

, где l - коэффициент трения.

Приравнивая оба равенства, получим: , откуда

,

где - число Рейнольдса, составленное по средней (расходной) скорости  и диаметру трубы D.



Выражение коэффициента сопротивления l как функции числа Рейнольдса () называется законом сопротивления ламинарного движения вязкой жидкости в цилиндрической трубе.

Необходимо отметить, что полученные соотношения пригодны для ламинарного течения только лишь на определенном расстоянии от входа в трубу, после исчезновения начального участка ламинарного потока (см. рис. 8).



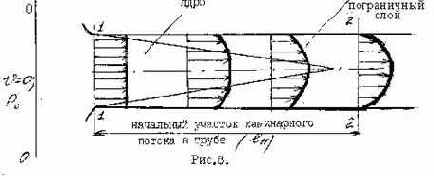
Если вход в трубу из резервуара выполнен достаточно плавно, то в на­чальном сечении 1-1 устанавливается практически равномерное распределе­ние скоростей. По мере движения жидкости тормозящее влияние стенок распространяется на всё большую толщу потока. На некотором участке, называемым начальным, поток имеет ядро, где сохраняется равномерное распределение скоростей, и пристенный пограничный слой, где скорости распределяются неравномерно. Сечение ядра вниз по течению убывает, а толщина пограничного слоя возрастает. В конце начального участка lн пограничный слой смыкается на оси трубы, и ниже по течению устанавливается параболическое распределение скоростей в соответствии с полученными соотношениями.

Этот характер течения и соответствующие ему зависимости имеют место только при устойчивом ламинарном режиме, т.е. при Re< Reкр. При  Re, немного меньших Reкр, в ламинарном потоке периоди­чески появляются кратковременные очаги турбулентности, которые могут на отдельных участках заполнять все сечение потока, образуя "турбулент­ные пробки".

При возрастании числа Re, турбулентный режим в каждом сечении существует все более длительное время и, наконец, поток становится турбулентным. Появление турбулентных очагов наступает тем раньше, чем больше возмущений испытывает поток при входе в трубу. Если вход сделать плавным и устранить другие источники возмущений, то ла­минарный режим можно получить и при больших числах Re  (напри­мер  20.000). Однако такие "затянутые" ламинарные режимы оказывались неустойчивыми, т.е. внесение в поток даже очень малых возмущений приводило к турбулизации.


Поэтому критические значения числа Re  следует понимать как границу устойчивого ламинарного режима в том смысле, что при. Re < Reкр любые внешние возмущения, вносимые в поток, будут с течением времени затухать и поток сохранит ламинар­ный характер. При Re > Reкр в зависимости от условий опыта может существовать ламинарный или турбулентный режим. Для круглых труб Reкр = 2300. Такое определение Reкр соответствует так назы­ваемому нижнему критическому числу Re.  Верхним  критическим числом Re называют то его значение, при котором устанавливается стабильный турбулентный режим.

2. МАТЕМАТИЧЕСОКЕ МОДЕЛИРОВАНИЕ ТУРБУЛЕНТНЫХ ТЕЧЕНИЙ

 ВЯЗКОЙ ЖИДКОСТИ

2.1. Переход ламинарного течения в турбулентное

Исторически первыми научными наблюдениями турбулентного дви­жения были опыты английского физика 0. Рейнольдса, в которых он в 1893 году изучал движение воды в круглой цилиндрической трубе [5]. При повышении скорости ламинарно движущейся жидкости было замече­но, как на подкрашенную и хорошо видимую вначале прямолинейную струйку начинают накладываться волны, распространение которых вдоль струйки говорит о появлении возмущений в ранее спокойном прямолинейном движении. Постепенно с ростом скорости воды число таких волн и их амплитуда возрастает, пока, наконец, струйка не разобьется на нерегулярные, перемешивающиеся между собой более мелкие струйки, хаотический характер которых позволяет судить о переходе ламинарно­го движения в турбулентное. Таким образом, с возрастанием скорости ламинарное движение теряет свою устойчивость, при этом случайные возмущения, которые вначале вызывали лишь колебания струек относительно устойчивого их прямолинейного положения, быстро развиваются и приводят к новой форме движения жидкости - турбулентному движению.

Если местная скорость  явно зависит от времени, т.е. изменяется с течением последнего, то движение и соответствующее ему поле скоростей называют неустановившимся или нестационарным. Если в каждой точке пространства вектор  имеет постоянное во вре­мени значение, то движение и поле скоростей будет установившимся или стационарным.


Если ламинарные течения могут быть как установившими­ся, так и неустановившимися, то турбулентные течения, строго гово­ря, всегда являются неустановившимися. Неупорядоченное движение частиц в турбулентном потоке создает резкие изменения местных ско­ростей во времени, называемые пульсациями скорости.

На рис. 9 приведено изменение местной мгновенной скорости uх турбулентного потока. Видно, что местная скорость изменяется во времени достаточно резко, однако ее значение колеблется около некоторого среднего. Поскольку использование в расчетах мгновен­ных скоростей приводит к труднос­тям, вводится понятие местной осредненной скорости:

,

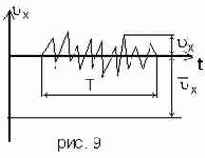где uх - мгновенная местная скорость, Т - период осреднения. Такой способ осреднения не является единственным, но благодаря прос­тоте его широко применяют в гидромеханике. При этом можно предполо­жить, что для каждого турбулентного движения существует такой доста­точно большой по сравнению с периодом турбулентных пульсаций постоян­ный период осреднения Т, что сглаживание по времени приводит к осредненной величине, при повторном сглаживании уже не изменяющей­ся, т.е. Если в результате осреднения, проведенного в данной точке в разные моменты времени t, будут получаться одни и те же значения uх , то осредненное движение называет­ся стационарным, а само турбулентное движение - квазистационарным. Разницу скоростей и  называют пульсационной скоростью или просто пульсацией: . Нетрудно убедиться, что осредненное значение пульсации равно нулю:



По правилу осреднения также следует, что среднее значение производ­ной от скорости по координате равно производной от среднего значения скорости по той же координате, т.е., т.к. опера­ции дифференцирования по координате и интегрирования по времени независимы. Таким же свойством обладает и производная по времени, т.е. . Все вышесказанное относится и к другим проек­циям скорости uу и uz

Правила осреднения обладают еще и следующими свойствами [6]:



 

 и т.д.

Величина , полученная в результате осреднения произ­ ведения двух пульсирующих функций ux и uy, носит наименование одноточечной (в знак того, что значения функций ux и uy при интегрировании берутся в одной и той же пространственно-временной точке) двойной корреляции, а отношение  - называ­ется коэффициентом корреляции между двумя статистически связанны­ми величинами. Равенство коэффициента корреляции R=±1 говорит о полной, детерминированной связи явлений, описываемых uх и uу (причем знак "-" говорит о противоположных фазах колебаний), а равенство R=0 говорит о статистической независимости явлений. Коэффициент корреляции между пульсациями, происходящими в двух раз­ных точках пространства и, вообще говоря, в различные моменты вре­мени, называется коэффициентом двухточечной пространственно - временной корреляции, причем, в зависимости от количества коррелируемых пульсирующих функций, двойной, тройной и т.д. корреляции.

Пульсационные составляющие скорости могут быть охарактеризованы частотой и амплитудой, которые при турбулентном движении изменяют­ся в широких пределах. В каждой точке турбулентного потока имеют место пульсационные скорости с целым спектром частот: от низких (5-10Гц) до очень высоких(50-100кГц). Средняя амплитуда пульсаций скорости характеризуется величинами равными: ; ; . Обычно степенью интенсивности турбулентности называют среднюю квадратичную величину скорости пульсаций, отнесенную к средней скорости потока:

 где .

Интенсивность турбулентности изменяется от 0.3% в атмосфере до 7-8% и более в машинах.

В своих опытах Рейнольдс впервые обнаружил, что переход лами­нарного движения в турбулентное обусловливается достижением критичес­кого значения некоторого безразмерного числа, или критерия, кото­рое в дальнейшем получило его имя. По опытам самого, Рейнольдса критическое число оказалось равным

 ;

здесь uср - средняя по расходу скорость, d - диаметр трубы. Впоследствии им же было открыто существование нижнего критического значения Reкр » 2000, такого, что при Re < Reкр движение в трубе оставалось ламинар­ным, каковы бы ни были введенные в течение возмущения.Вместе с тем было замечено, что путем удаления возмущений на входе в трубу или уменьшения начальной их интенсивности можно искусственно затянуть ламинарное движение в область значительно бóльших значений числа Re, например, до 5×104. Конечно, такое затянутое ламинарное движе­ние не терпит появления даже очень небольших возмущений и сразу же переходит в турбулентное.


Содержание раздела

---